Finding the track lanes, Part III
As a quick recap from last time, we started with this image:
and using some processing we got to this: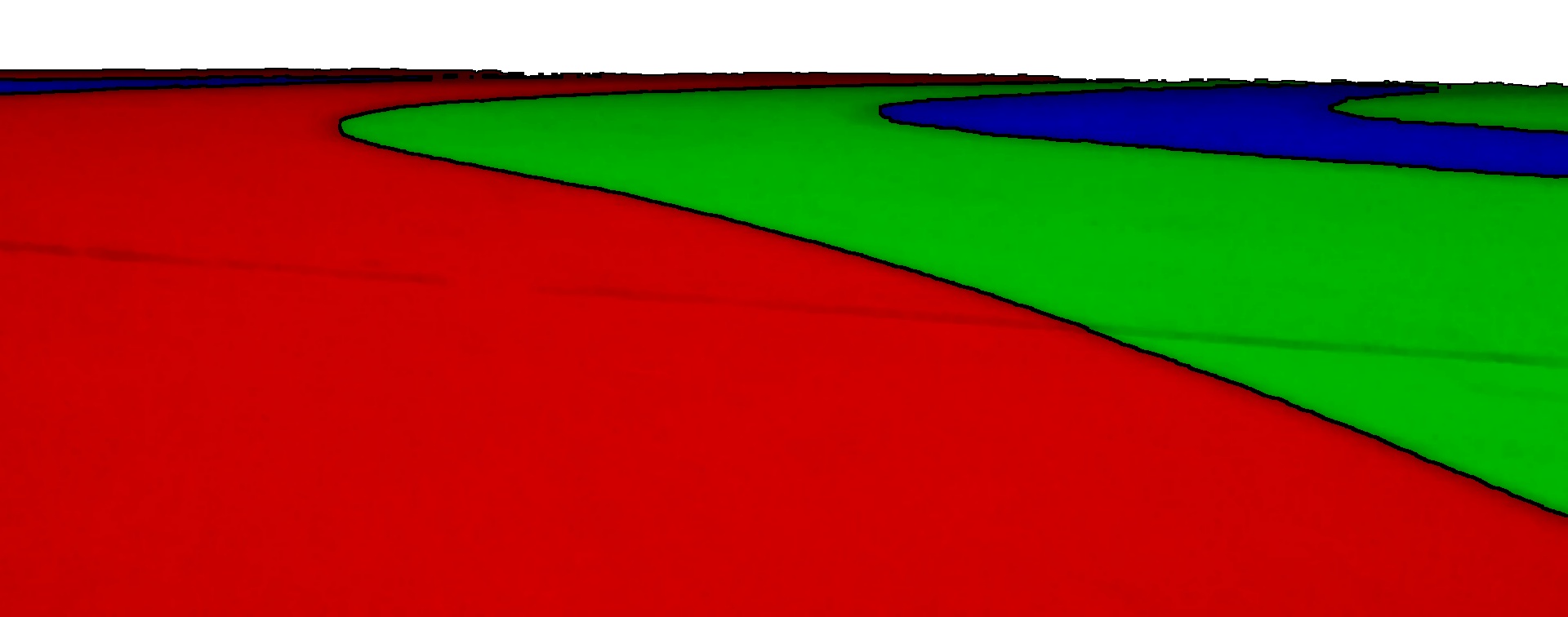
then we did some further processing to arrive at some points:
We will be continuing the code from the previous part, which you can find here:
Finding the track lanes, Part II
For those who have access to the full Race Code now you will notice that parts I and II show how the StreamProcessor.ProcessImage function does its job.
From this point on there is no more image manipulation to do, we are in to maths territory now :)
We are at the stage that StreamProcessor.SetSpeedFromLines takes over.
From the end of previous part we package up the matched points into a list of lists like this:
lines = [matchRW, matchRB, matchRG, matchGB, matchGW]
We will pass this on to the next stage and we can throw everything else we worked out away now.
This is the same basic set of results returned from the Race Code Function: TrackLines().
The only difference is there is one list per edge, making a total of 7 lists instead of 5.
The first thing we do is pick a line to work with.
While it would be more accurate to use as much data as possible, it is quicker to use a single line.
In our case we decide to go with the line that has the largest number of available points.
We can do that quickly by comparing the list lengths like so:
count = 0 index = 0 for i in range(len(lines)): if len(lines[i]) > count: index = i count = len(lines[i])
This gives us a count of 49 and an index of 2.
The count is how many points are in the line, 49 in this case.
The index is which line it was, in this case lines[2] which is matchRG.
To determine where we actually are on the track the code needs to know which lane this is.
We can build a simple lookup table to determine the lane like this:
lineIndexToOffset = {
0 : +3.0,
1 : +1.0,
2 : 0.0,
3 : -1.0,
4 : -3.0
}
we can then use our index number to get the lane offset and the line to use:
lineOffset = lineIndexToOffset[index] bestLine = lines[index]
In this case we are looking at the center lane, so lineOffset is 0.0.
What we also need to know is how far away from the line we are.
Looking at the line again:
we can see that varies through the image.
There are a few different ways of approaching this problem.
Two good ways are:
- Take an average of where all the points are
- Take the point at a position in the image
Option 1 is potentially more accurate, but it can get confused by curves and parts of the image which are hidden.
Option 2 is simpler, but it can get confused if there is no point near enough to the position we are looking for.
As we have a large number of varying curves along with robots which can block our view we will use option 2.
This means we need to decide on a position in the image, ideally a bit ahead of where we are.
We will go for 33% of the way down the image, which is here:
To do this we want to work out what Y value this corresponds to like so:
targetY = (cropBottom - cropTop) * 0.33
Which works out at approximately 249.5.
The next thing to do is find the point closest to this target.
This is very similar to the search for the best line to use:
offsetIndex = 0 offsetErrorY = abs(targetY - bestLine[0][1]) for i in range(len(bestLine)): errorY = abs(targetY - bestLine[i][1]) if errorY < offsetErrorY: offsetIndex = i offsetErrorY = errorY offsetPoint = bestLine[offsetIndex]
This returns the closest point to our target line:
In this case it is at (805, 248).
Now we have our point we need to measure how far out it is.
To do this we need an X position we are aiming for and we need to know how far apart the lanes are.
We have worked these out as:
targetX = width / 2.0 laneWidth = 1250.0
The lane width is dependent on the targetY value and resolution.
We worked it out by getting a photo at the correct size with two straight edges in shot and measuring the X difference at the target Y position.
The targetX value is where in the image you want to 'aim' for, in our case central.
We now want to measure the X distance to the target:
offsetX = offsetPoint[0] - targetX
Then see how it compares to a whole track:
offsetX = offsetX / laneWidth print offsetX
We get -0.124, this means we are about 12% of a lane to the right of the line we are looking at.
We can compute the full track offset by summing the offset of the line from center with the offset from the line.
In our case:
trackOffset = lineOffset + offsetX print trackOffset
Gives us -0.124, this means we are about 12% of a lane to the right of the center of the track.
This is the value we return from CurrentTrackPosition():
At this point we have enough information to perform a basic line following algorithm.
To improve things further we want to look at where the track is heading in front of us.
Stay tuned for Part IV where we figure out how we can determine what the track itself is doing.


Add new comment